추상대수학

개발자로써 간단히 개념 공부한 것을 적어놓는 공간

• 참고자료
  nLab (강추!)
  추상대수학 책
  위키백과
  alice_college_math_lecture.pdf

카테고리 이론 (범주론, Category theory)

범주론은 수학의 일반적인 추상 구조를 설명하기 위한 tool set이다.

집합론과 다른 점은 집합론은 객체에 초점을 맞춘다면 범주론은 객체간의 관계에 초점을 맞춘다.

카테고리 (범주, Category)

형태소 (morphisms)

군 (group)

군이란 결합적 연산을 갖고, 이 연산에 대해 항등원을 가지며, 모든 원소가 역원을 갖는 집합으로 정의한다.

군은 *<G, > 일때 다음 공리들을 만족하는 연산 *를 가진 집합 G를 말한다.

1. *는 결합적

2. G의 모든 원소 a에 대해 ae=a 이고 ea=a인 원소 e가 G에 존재한다.

3. G의 모든 원소 a에 대해

   $$a\ast a^{-1}=e및a^{-1}\ast a=e를만족시키는원소a^{-1}가G안에존재한다.$$

   정수의 덧셈군: $<\mathbb{Z},+>$, ℤ

   정수의 곱셈군: $<{\mathbb{Z}}^{\ast },•>$, ${\mathbb{Z}}^{\ast }$

   '0이 아닌 정수, 유리수, ...'의 집합: ${\mathbb{Z}}^{\ast },{\mathbb{Q}}^{\ast },...$

   유리수의 덧셈군: $<\mathbb{Q},+>$, ℚ

   유리수의 곱셈군: $<{\mathbb{Q}}^{\ast },•>$, ${\mathbb{Q}}^{\ast }$

   군은 모든 원소가 가역원인 모노이드이다.
   

유한군 (finite group)

응용 과학에서 많이 쓰임. 유한개의 원소만을 갖는 군.

예)

G: 6을 법(modulo)로 하는 ℤ (정수군)

덧셈을 하면 4+3의 경우 1이 된다. 4+2 의 경우 0

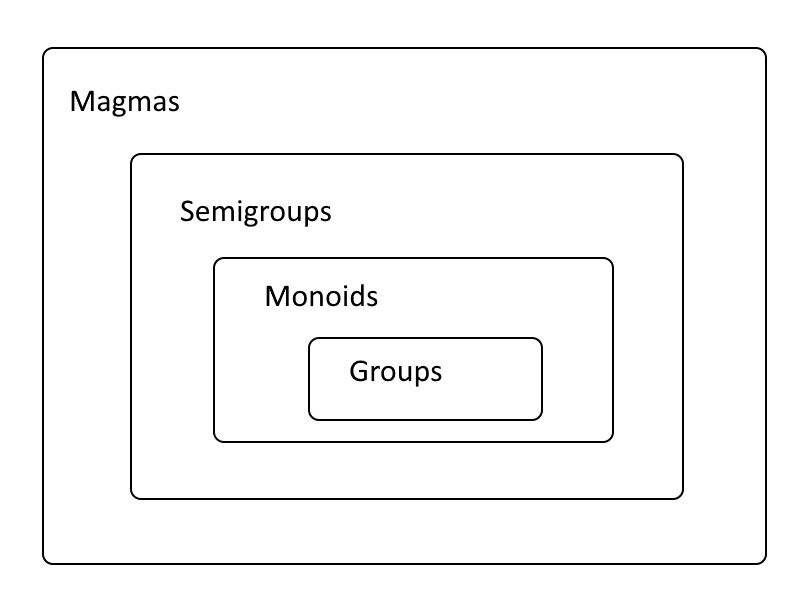
마그마(Magma)

집합S에 대해 S×S → S를 만족

(S, ∙)

반군 (subgroup, semigroup)

위의 마그마를 만족하며

S가 닫혀있고(closed) 결합법칙을 지킬때의 이진연산

모노이드(monoid)

반군에서 항등원을 가지고 있는 그룹. 2가지 명제를 더 가지고 있음.

<M, *>에서 다음과 같은 식을 만족시킨다.

Right identity(오른쪽 항등식): $x\ast e_R=x$

Left identity(왼쪽 항등식): $e_L\ast x=x$

항등원을 가지고 있기 때문에 항등원을 넣으면 X → X가 가능.

monoid-스러운 category를 monoidal이라고 한다

어떤게 monoidal한가?

Category C에 C * C -> C (즉, C의 원소의 쌍을 원소로 가지는 Category에서 C로의) Functor ★가 있어서 C의 항등원 $e$랑 같이 다음과 같은 성질을 만족하는 걸 말합니다

C의 아무 원소 a, b, c에 대해서
★(a, $e$) = a
★($e$, a) = a
★(a, ★(b, c)) = ★(★(a, b), c)

여기에 잘 설명되어 있다.

Monoidal category - Wikipedia

Cayley식 표현 정리

모노이드는 집합 M에서 (M, ⊕, e)이고,
결합적인 이진 연산 ⊕ : M × M → M((a ⊕ b) ⊕ c = a ⊕ (b ⊕ c))이며,
요소 e ∈ M은 이항 연산과 관련하여 왼쪽과 오른쪽 항등원입니다(즉, e ⊕ a = a = a ⊕ e.).

명백한 모노이드(N, ·, 1)로 인해 이항 연산 ⊕과 요소 e는 종종 모노이드의 곱셈과 단위라고 불립니다.

모든 집합 M에 대해 우리는 동형(endomorphisms) 모노이드(M → M, ◦, id)를 구성할 수 있습니다.
(자세히 보면 가운데가 뚥린 원) 여기서 ◦는 함수 구성이고 id는 항등 함수입니다.

injection이 있는 경우 M은 모노이드의 서브모노이드(M', ⊕', e')입니다.
$i:M\hookrightarrow M^{\prime }$ 즉 일부 ⊕ 및 e에 대해 i(e) = e' 및 i(a ⊕ b) = i(a) ⊕' i(b)입니다.

증명

1. 이진 연산 ⊕을 커링하여 주입 표현 M → (M → M)을 구성합니다.
   $rep(m)=\lambda m\prime .m\oplus m\prime .$

2. 함수 ref는 모노이드의 형태이다.
   $rep(e)=\lambda m\prime .e\oplus m\prime =id$

$rep(a\oplus b)=\lambda m\prime .(a\oplus b)\oplus m\prime =\lambda m\prime .a\oplus (b\oplus m\prime )=(\lambda m.a\oplus m)◦(\lambda n.b\oplus n)=rep(a)◦rep(b)$

자연 변환(natural transformation, $u$)

두 함자 사이에 범주적 구조를 보존하는 변환

category of functor은 군C → 군D 을 만족시키는 Functor F, G, … 를 카테고리로 묶은 것이고,

이 중에서 C의 두 원소 a, b 사이에 mapping f : a -> b가 있을 때,
u(b) . F(f) === G(f) . u(a)여야 한다.

를 만족시키는 것을 자연 변환 u : F -> G 라고 한다.

일단 제일 뻔한(?)건 한 Functor F에 대해 u : F -> F인 애인데

F가 C에서 D로의 Functor라고 하면

C의 모든 원소 a에 대해
u(a) = id(F a)

모나드(monad)

자기 함자 모노이드

Monads are just monoids in the category of endofunctors

category of endofunctors의 monoids이다.

닫혀있음(closed)

닫혀있다는 것은 임의의 군(group) G, f, g∈G, 임의의 연산 *라고 했을때 f ∘ g = z에서 z는 z∈G 만족시킨다는 것이다.

아벨군(abelian group, 가환군, commutative group )

군에서 추가로 교환법칙이 성립할때.

모든 $g,h\in G$ 에 대하여 (G, *)에서 $g\ast h=h\ast g$ 처럼 가환을 만족시키는 군이다.

환

가군(module)

집합(set)

특정한 조건에 맞는 별개의 원소들의 모임

어떤 대상이 집합에 속하는지 여부는 명확해야 하며, 집합 위에는 순서나 연산 따위의 구조가 주어지지 않는다.

• 수의 집합

  

ℕ, ℤ, ℚ, ℝ

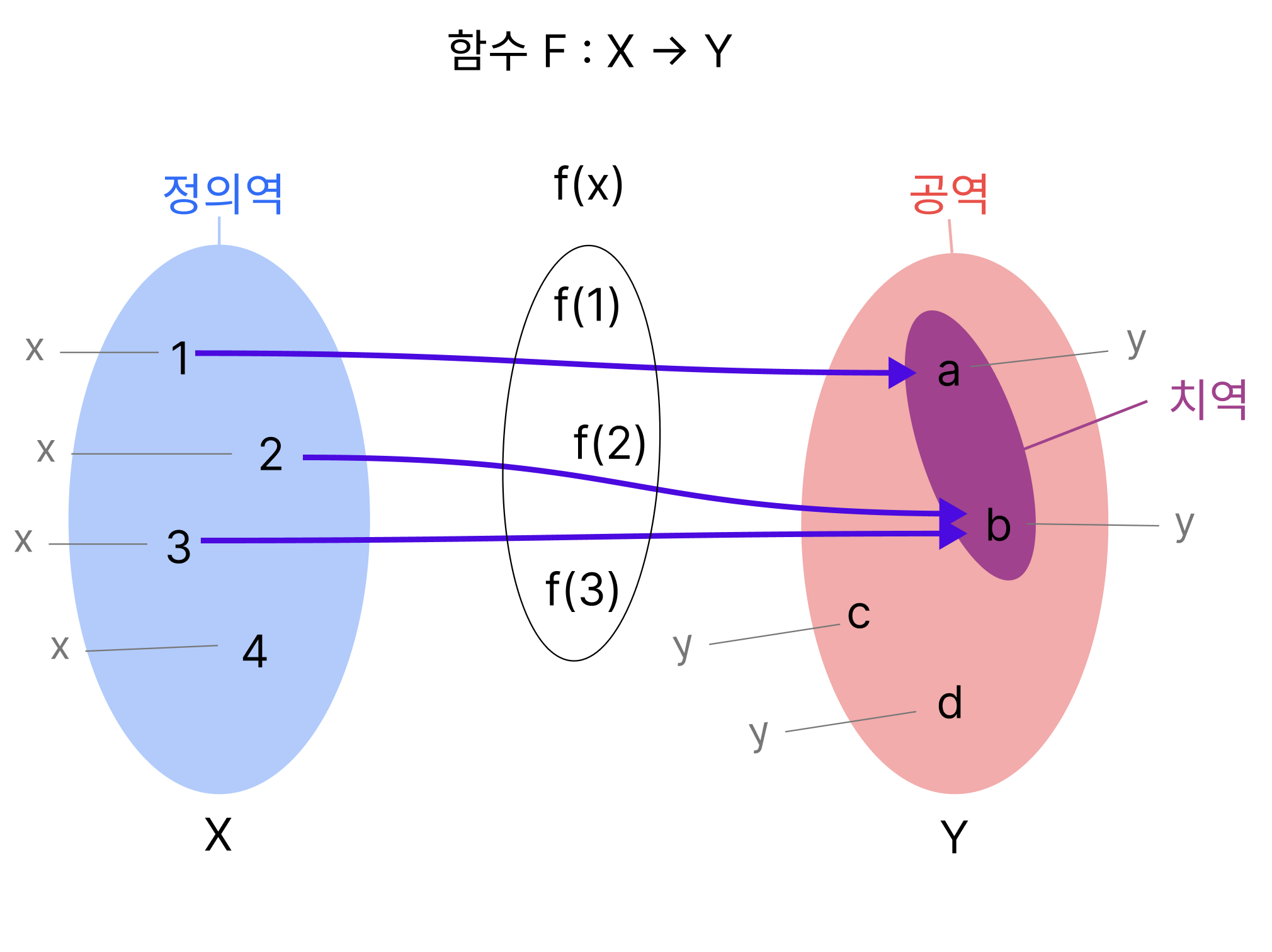
정의역(domain), 치역(range), 공역(codomain)

f: X → Y에서

정의역: X.

공역: Y

치역: Y에서 정의역에 대응하는 영역

치역은 공역의 부분집합이다.

위수 (order)

군이 유한군일때 원소의 갯수

G가 유한군이면 G의 원소의 개수를 G의 위수라 부름.

기호: |G|

사상(Morphism)

수학적 구조를 보존하는 함수의 개념을 추상화한 것이다. 예를 들어 집합의 사상은 임의의 함수이며, 군의 사상은 군 준동형, 위상 공간의 사상은 연속 함수이다.

사 는 복사의 뜻이고

상 은 형상, 이미지라는 뜻이다. 물체를 복사하듯 구조를 보존하는 대응이다. 구조를 보존한다는 것은 연산의 구조 또한 보존한다는 의미가 있다.

어떤 변환을 맵핑이라고 부를 땐, 구조를 완전히 보존하는 일대일대응인 경우가 많다.

사상은 단순히 대상들 사이의 '화살표'일 뿐이다.

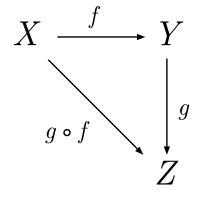
왼쪽 그림에서 f, g는 사상이며

사상 f, g의 합성을 f∘g 또는 fg라 한다.

자기 사상(Endomorphism)

정의역과 공역이 같은 사상

${\displaystyle f:X\to X}$ 와 같이, 시작과 끝이 같은 사상을 자기 사상이라고 한다.

함자(Functor)

두 범주(category) 사이의 함수에 해당하는 구조로, 대상을 대상으로, 사상을 사상으로 대응시킨다.

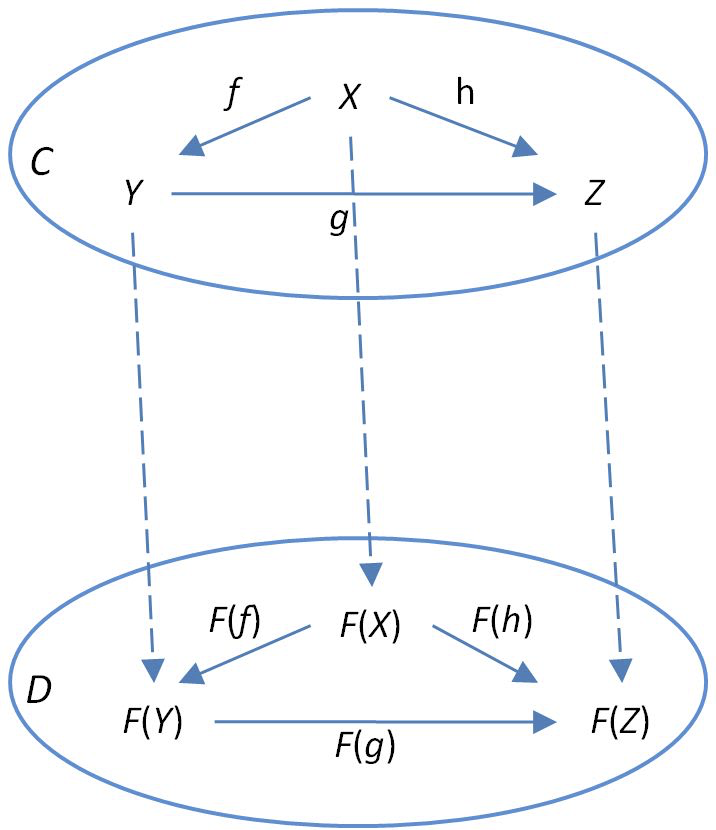
엔도펑터(endofunctor)

fmap :: (a -> b) -> (f a -> f b)

• fmap id == id (preserves identities)
• fmap (f . g) == fmap f . fmap g (preserves composition)

를 범주에 매핑하는 펑터 (haskell의 모든 펑터는 endofunctor다)

시작 category와 목표 category가 같다.

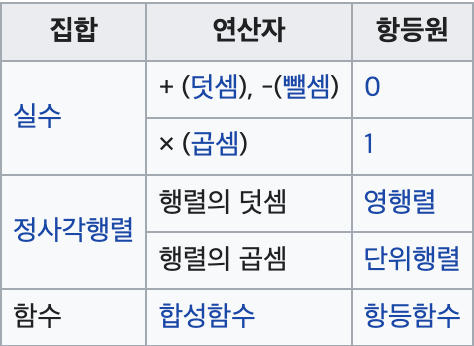
항등원 (identity element, neutral element, 단위원)

임의의 수 a에 대하여 어떤 수를 연산했을 때 처음의 수 a가 되도록 만들어 주는 수

집합 S와 S에 대해 닫혀 있는 이항연산 *로 이루어진 마그마 (S, *)가 주어졌을 때,

모든 군에는 항등원이 오직 하나만 존재할 수 있다.

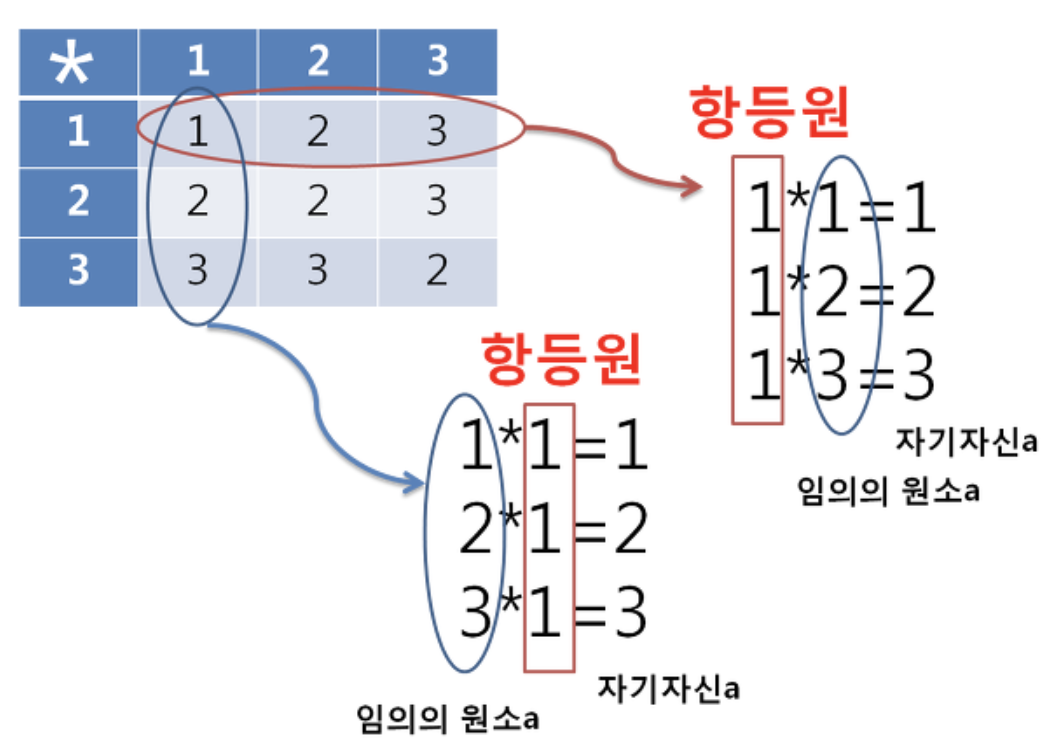
예)

역원 (inverse element)

집합 S와 이항연산자 *에 대해, 만약 항등원 e가 존재한다고 할 때

S의 원소 a에 대해 ab = ba = e를 만족하는 S의 원소 b가 유일하게 존재할 때

b를 a의 역원이라고 한다.

모든 군에서 각 원소의 역원은 단 하나만 존재할 수 있다.

예)

덧셈 역원: 더했을때 0이 되는 수

→ 7의 반수는 -7

*이항 연산 (binary operation, ∘, , +)

집합 S에 닫혀 있는 이항 연산일때,

삼항연산부터는 정의할 의미가 없는 게, A + B + C 같은 연산은 일단 A + B 를 구한 뒤 거기다가 + C 를 하면 되기 때문에 결국엔 이항연산으로 환원된다.

세분 (Refinement)

가역원 (invertible element, unit)

환 또는 모노이드에서 곱셈에 대한 역원이 있는 원소들이다.
집합 M에 대한 **가역원군(가역원의 군)**을 Unit(M) 이라 표현한다.
예)

모노이드 M의 원소 x ∈ M의 역원 y는

$xy=yx=1$

이 되는 원소 y ∈ M이다.

반수(덧셈 역원, 반대수, opposite number)

덧셈에서 절대 값은 둔 체 부호만 바꾼 수

연산 (operation)

임의의 집합 A 위에서의 연산은 A의 원소들의 순서쌍(a, b)마다 단하나의 A의 원소 a*b를 대응하는 규칙. 연산 결과가 해당 집합 A에 머물러 있다면 닫혀있다(closed)라 한다.

가환 (교환법칙, commutative)

ab = ba
순서쌍의 두 원소의 순서가 상관 없음

결합적 (결합법칙, associative)

(a**b)*c = a(b*c)

함수(function)

X,YB가 집합일때, A의 각 원소 x에 대해 B의 유일한 원소 y를 대응하는 규칙을 X로 부터 Y로의 함수라고 한다.

이 관계를

y = f(x)

처럼 나타내는데. y를 함수 f에 의한 xi의 상(image)라고 한다.

f: X → Y

X는 정의역(domain) Y는 치역(range), 정의역에 대응하는 영역은 공역(codomain). 공역은 항상 치역의 부분집합이다.

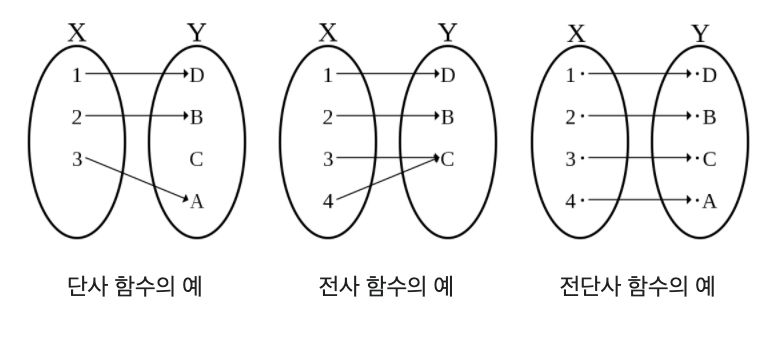
함수를 정의할때 정의역과 공역은 무조건 필요하다.

단사(injective, one-to-one) 함수

둘 이상의 원소가 동일한 상을 가지지 않는다면 f는 단사 함수이다.

전사(surjective) 함수

B의 각 원소가 적어도 한개의 A의 원소의 상이면 f는 전사 함수이다.

전단사(one-to-one correspondence) 함수

A의 원소와 B의 원소가 정확히 한개의 짝을 가질때

일대일 대응이라고도 부른다.

합성 함수(com-posite)

A → B → Z에서

f: A → B

g: B → C

라고 할때

f∘g: A → C

$모든x\in A에대해[g\circ f](x)=g(f(x))$

f와 g가 단사 함수이면 f∘g도 단사 함수이다.

f와 g가 전사 함수이면 f∘g도 전사 함수이다.

f와 g가 전단사 함수이면 f∘g도 전단사 함수이다.

역함수(inverse function)

f의 역원은 $f^{-1}$라고 한다.

$f:A\to B$

$f^{-1}:B\to A$

항등함수(ℇ, identity function)

집합 A에 대한 항등함수 기호: ${ℇ}_A$

임의의 집합 A에 대해 A의 모든 원소를 자신에게 보내는 함수. x → x

정의역과 공역이 같고 모든 원소를 자기 자신으로 대응시킴.

ℇ이 A의 치환이다. 즉 A와 자신 사이에 일대일 대응을 보인다.

그렇다면 다음이 성립한다.

$f\circ ℇ=f및ℇ\circ f=f$

그리고 f가 A의 임의의 치환이고, $f^{-1}$가 역함수일 때 다음이 성립한다.

$f^{-1}\circ f=ℇ및f\circ f^{-1}=ℇ$고

대수 (algebra)

수학 대신에 문자를 사용하여 대수적 구조를 연구하는 학문
예를 들어 미지수 $x$ 라고 하는 것도 대수이다.

우리가 정규 교육시간에 지겹도록 배운 공식들은 **대수식(Algebraic Expressions)**이라고 한다.

대수적 (algebraic)

대수적이다는 모여 있는 구성원들 사이에 연산이 존재하고, 일정한 규칙을 따르는 것이다.

대수 타입 (ADT, Algebraic data type)

범위에 따라 다르다.

크게 보면 서로 다른 타입들끼리 어떤 식으로든 관계가 맺어져 새로운 타입을 만드는 것.

Union(합), And(곱) 타입도 포함된다.

개발쪽에서 ADT라 함은 보통은 제네릭 타입을 포함하는 타입을 말한다.

타입스크립트 예제로 치면 다음과 같다.

interface Eq<T> {
  readonly equal: (a: T, b: T) => boolean;
}

프로그래머적 관점

사상

사상은 그냥 타입(클래스, 인터페이스 등)에 대한 함수나 마찬가지다.

예를 들어 string의 경우 string 자체가 category이기 때문이다.

functor

예를 들어 f: A → B이면 A을 넣었을때 B가 나와야 한다.

어떨땐 B가 나오고 어떨땐 C 나오고… 이러면 functor의 조건을 만족시키지 못함.

endofunctor

예를 들면 f: A → A 처럼 동형이 나오는 것이다.

시작 범주랑 끝 범주가 같으므로 endofunctor를 무한히 이을 수 있다.

이 성질과 monoid의 성질이 합쳐짐으로써 monad가 왜 그렇게 강력한지 알 수 있다.

category of ~

category of functor 처럼 말하면 말 그대로 펑터의 카테고리이다.

마그마, 반군, 모노이드, 군, 모나드

프로그래밍에서 이 넷은 전부 이진연산에 해당한다. 거창한 개념은 필요 없다.

마그마(Magmas) → 닫혀있는 이진 연산

반군(Semigroups) → 마그마 + 결합법칙을 지킬때 (foldl, foldr시 동일한 결과 제공)

모노이드(Monoid) → 반군 + 항등원을 가지고 있을때

군(Groups) → 모노이드 + 역원을 전부 가지고 있을때

모나드

위의 추상대수학에서 모나드는 자기 사상 함자 모노이드라 하지 않았는가? 결국 모나드는 닫혀있고 결합법칙을 준수하고 항등원을 가진 이진 연산인데 함자를 대상으로 한 자기 사상적 결과가 나오는 개념이다.